Colleagues:
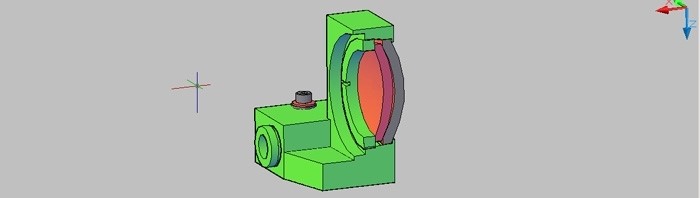
Well, with Summer around the corner this may be my last chance to tickle your consciousness before the lazy days set in. My subject this time is broken flexures, specifically broken double cantilever blade flexures of the sort shown:
I have long been reluctant to use this type of flexure because the double cantilever beam, being restrained on both ends, is not well described by linear elastic structural theory. Rather than study the problem I’ve just avoided it, until now. The difference between now and then is that a friend has some broken double cantilever blade flexures now and has sought my counsel. Well, one thing leads to another and here I am: With a friend who has broken flexures. Way back then broken double cantilever blade flexures were less personal, just conjectural. I was able to avoid the whole issue. But, now is now so here I go.
The “problem” with the double cantilever beam, and the flexures that rely on its mechanics, is they don’t fit “well” into the small displacement linear elastic theory that is usually used to analyze them for strength and stiffness. As I will show it all depends upon what you may call a “small displacement.”
As you deflect the double cantilever beam flexure by applying a load in the center, the center will deflect and the length of the beam will increase, at first slowly and then faster and faster. This increase in length creates axial forces and tensile stresses in the beam (flexure). This increase in length is a second order effect in the differential equations and therefore ignored by the small displacement linear elastic theory. The Euler-Bernouli beam theory agrees with the finite element method that these tensile forces and stresses do not exist. But intuitively they have to be there. How severe is this discrepancy?
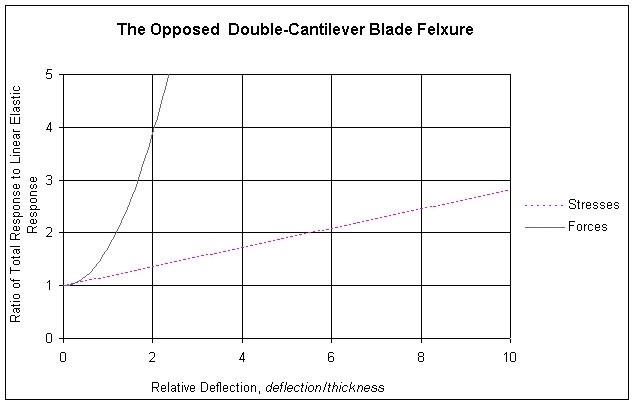
I take as my starting point some earlier work (Hatheway, SPIE, 3132-19, 1997) on the radius of curvature of the locus of the end point of a cantilever beam. This permits the calculation of the foreshortening of a free cantilever beam, which would be equal to, and opposite in sense to, the stretching in a constrained cantilever beam. With this information I was able to estimate the forces and stresses attributable to the stretching of the beam (flexure). These need to be added to the Euler-Bernouli results. They are shown in the following chart, the vertical axis of which presents a ratio which is the sum of the Euler-Bernouli bending effect and the non-linear stretching effect divided by the Euler-Bernouli bending effect alone. The magnitude of the ratio is shown for both stress effects and force resultant effects. The horizontal axis is the deflection of the flexure as a multiple of the thickness of the flexure’s blade.
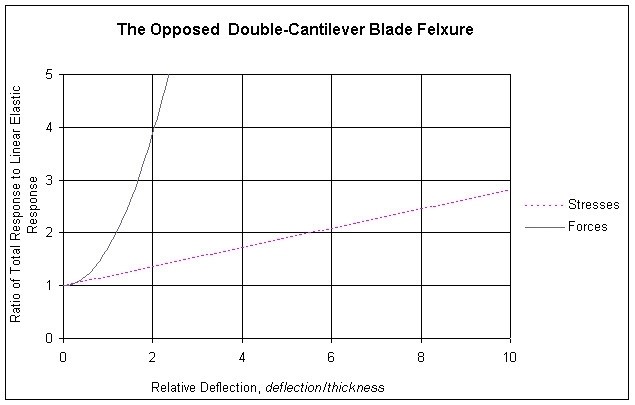
As you may observe the stresses and forces agree
reasonably well with the linear elastic stresses and forces when the
deflections (and therefore the Relative Deflections) are very small,
approaching zero. When the deflection approaches the thickness of the
blade (Relative Deflection equal to 1.0) the state of stress is about 18%
higher (Ratio=1.18) than the linear elastic stresses alone and the reaction
force is about 72% higher (Ratio=1.72) than the linear elastic bending load
alone. From there the values increase, the force values quite rapidly.
Thus, for a given deflection the designer may estimate the total force and the
total tensile stress in the flexure: First, from the required deflection,
calculate the linear elastic values for stress and force from conventional beam
theory (or a finite element model). Then multiply these by the factors
from the chart. These are still “small displacement” results, but
“nonlinear” as you can see, incorporating only one higher order or
higher degree term in the solution. (A caution: It is not at all
clear that these are valid all the way out to a Relative Deflection of
10. Other higher order terms surely will contribute somewhere in this
range.) One open question is then, “Just how small is the small
displacement domain?” One answer might be based upon desired
accuracy. Another might just seek to satisfy some required Factor of
Safety. Obviously, if the displacements are small enough one needn’t
worry about non-linear effects (Or any effects at all, a wag might point out!).
Well, that’s kinda’ what I’ve been up to this Springtime. And now, with
the weather warming up and a fresh tube of sun-block I’m ready to let you
go.
But first — I’ve been invited to address the Optical Society of
Southern California (OSSC) at their dinner meeting on June 23rd. My
subject will be “Applying the Arts of Structural Engineering to
Optics.” It is an open meeting, anyone may attend, but you must make
reservations if you’ll be there for dinner. I promise to be more
entertaining than this dry missive.
For reservations go to
http://www.ossc.org
The meeting will be at Luminaria’s Restaurant in Monterey Park, near the
intersection of Interstate 10 and Interstate 710. I expect to be
challenged on the relevance of the “linear small displacement
domain,” other charming topics and I look forward to a vigorous
discussion. Hope to see you all there.
Al H.
6-7-10