Colleagues:
AEH has solved elastic
theory’s differential equations for the tensile stresses in glass lenses
mounted in threaded metal rings, and it’s
good news.
Paul Yoder had originally proposed Delgado and Hallinan’s 1975 solution (Opt.
Eng. 14) but their solution gave very high tensile stresses in the
lenses, high enough that virtually all such lenses should have fractured.
None of my ring mounted glass lenses had ever suffered that fate. I
surveyed a number of my colleagues and none of them recalled a ring mounted
glass lens fracture.
Delgado and Hallinan’s work was flawed. To correct their flaw would
require a new solution to the equations of elasticity that honored the
appropriate contact geometry. AEH
finally made it happen and the result is surprisingly simple,
s = p(1-2u)/b,
where s is the peak tensile stress, p is the
linear ring load, b is the radius of the contact ring and u is
the Poisson’s ratio of the glass. This stress is three-to-four orders of
magnitude lower than that predicted by Delgado and Hallinan.
Using Nastran AEH was also
able to verify the general shape of the stress distribution in spite of
Nastran’s notorious difficulty at the point of load application.
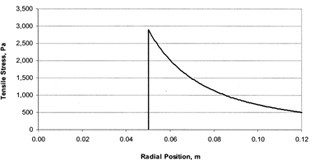
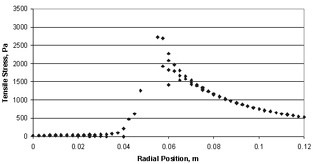
Closed-form solution >>> Nastran solution
To learn more you have choices: Either download AEH’s peer reviewed paper from SPIE [Optical Engineering 57(5), 055105] or go through the gory details with me in my tutorial,
“Optomechanical Analysis,”
SPIE’s Optics and Photonics Symposium in San Diego
8:30 AM to 5:00 PM on the 21st of August.Cheers!
Al H.
6-6-18