Dear Colleagues:

I have recently been involved in lively discussions about the nature of glass as a structural material and how to predict its strength properties.  The fact is that glass is by nature one of the strongest materials on earth with a “native” tensile strength on the order of 500,000 psi, stronger than most high alloy tool steels.  So, I am asked, “Why do the glass suppliers say to keep the stresses under 1,000 psi?”  The answer is that, unlike steel, glass is completely brittle showing no perceptible plastic deformation whatever in it its fracture. 

The growth of cracks in stressed steel parts is arrested by the plastic deformations in the material at the tips of the cracks.  The plastic deformations produce a small radius at the tip of an otherwise sharp crack, thereby reducing the high concentrated stresses (by orders of magnitude) at the very tip of the crack.

The growth of cracks in stressed glass parts is not arrested since plastic deformation does not occur.  This does not mean however that the strength of glass is indeterminate, unknowable or a random property.  It does mean that you should expect that glass has slightly different behavior than the ductile structural materials like steel.

It has been shown by a number of researchers that under tensile stress a crack in glass will tend to grow in length (or depth) at a rate that is proportional to the nominal stress at the tip, s, and proportional to the square-root of its length, d.  To quantify the influences of stress and crack length on strength properties, structural engineers have developed a quantity known as the “stress intensity” that is usually represented by the character “K1.”  K1 includes a coefficient, a, that accounts for the geometric shape of the crack and is defined as,

K1 = s(ad)^.5

A crack propagation curve for fused silica is shown in the figure.

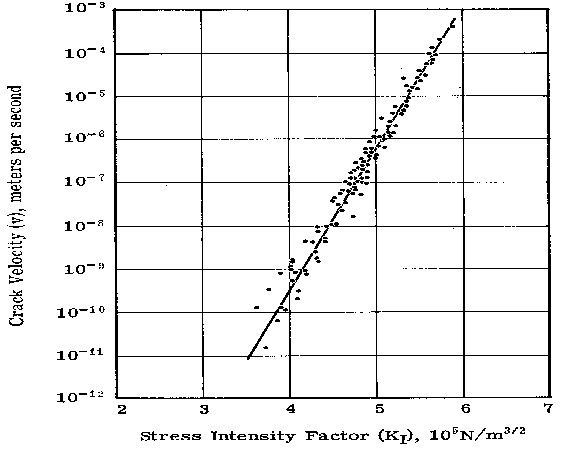
Other glasses may have different, even zig-zag, curve shapes.

It has also been shown by researchers that the crack will continue to grow in this predictable fashion until the stress intensity reaches a critical value, K1c, at which point the crack growth becomes unstable and proceeds rapidly to complete fracture without a velocity limit (except, perhaps, the speed of sound in the glass).  The critical stress intensity, K1c, is often published as the material strength property for a glass, ignoring the propagation effects above.

Glasses, especially optical glasses melted and cooled in a boule, are very uniform, isotropic and crack-free in their as-cooled state.  They exhibit the high “native” strength described above.  The cracks we are talking about here are all produced in subsequent fabrication processes: single point turning, grinding, polishing, etc., all of which produce sub-surface cracks that are about three time as deep as the diameter of the abrasive used in the process.  Polishing may remove visible grinding pits that are about as deep as the abrasive but may also leave behind invisible subsurface cracks that can still be twice as deep as the abrasive grinding grit.  “Controlled grinding and polishing” is the art of reducing and/or minimizing these residual subsurface cracks by special fabrication techniques.
 
So, this is the physics:  Ground and polished glass parts with structural stresses in them all have finite service lives because the cracks will grow continuously until complete fracture.  The lower the stress, the longer the life will be.  At 1,000 psi and with common optical finishing processes, the parts life may approach the human life span, sufficient for most cases and often recommended by glass suppliers.

As an engineer it is my practice, at higher stress levels, to integrate under the crack propagation curve to determine the acceptable fabricated crack length, d, in a glass part exposed to a known stress history and with a required service life.  The lower limit of integration is the stress intensity, K1i, at the initial as-fabricated crack length and the upper limit is the critical stress intensity, K1c.  This calculation provides the user with an assured minimum lifetime for his product.  It also lends itself to definition of non-destructive proof-testing for finished products to demonstrate the safe service life of each one. 

I perform the integration in custom software that I call Crystal. 
Crystal accommodates arbitrarily-shaped propagation curves and time-varying loading. 

One “snag” is that glass producers have not been encouraged to publish crack propagation curves for their glasses so the data are fairly sparse.  On the up-side however there is sufficient published data that a safe envelope for similar types of glass may often be assumed.
 
So, this is the engineering:  respect the physics and avoid broken glass.

Now…  Springtime is here and the snows will melt.  Yes, even in Spokane and Burlington!

Cheers. 

And no more broken glass!  OK?

Al H.
4-11-08