Colleagues:

Some of you may remember a survey I conducted a couple of years ago concerning the fracture of ring-mounted glass lenses.  Of the 300 or so optical professionals queried (OSSC and SPIE members, mostly) not one had first-hand experience in such a mounting failure.  Several expressed grave concern and one or two had heard stories that they felt were creditable.  This group must have personally guided thousands of lens mount designs.  And not a single fractured lens among them.  This basically validated my experience:  I’ve never had a ring-mounted glass lens fracture because of its mounting.

The anomaly here was that the accepted structural theory (Delgado and Hallinan, Opt. Eng. 14, S11, 1975) predicted very high tensile stresses in the lenses, especially at low temperatures when the metal contracts more than the glass.  Many failures should have been reported, especially in the military sector where low temperature operation is required.

The good news is that the accepted structural theory was wrong.  Those authors accepted that the contact between a sphere and a flat plane is the same as the contact between a ring and a flat plane.  The stresses in the sphere-on-plane case had been solved by others whereas the stresses in the ring-on-plane case would take some additional development effort.

Now, the ring-on-plane case has been solved (Hatheway, Proceedings of SPIE, 7424-14, 2009) for the surface tensile stresses that may cause fracture. 

For comparison lets take a lens cell I designed a short while ago.  The lens is 10 cm diameter and needs a ring compression load of 77.3 N to secure it against a shock load of 20 gs. 

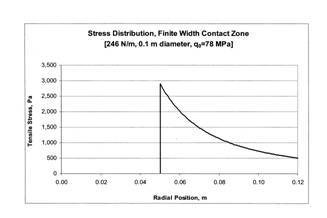
The peak tensile stress according to the sphere-on-plane theory is

s=15,300,000 Pa (2,238 psi)                             (Delgado and Hallinan)

and the peak tensile stress for the ring-on-plane theory is

s=2,893 Pa (0.422 psi)                                  (Hatheway)

a ratio of 5,300:1, almost four orders of magnitude.  The higher level (2,238 psi) is enough to cause fracture in a short period of time (about three minutes).  The lower level (0.422 psi) would provide a lifetime longer than the engineer who designed it (10.3 x 10¹⁴ years) and possibly account for the lack of witnesses in my survey, above.

Those of you interested in the gory details can download my paper from the SPIE website.  Please don’t ask me for copies because I’ve signed the copyright over to SPIE.  However, as a consolation prize for reading this email all the way through I’ll give you the answer:

Peak tensile stress=P(1-2u)/2pr²

where P=ring loading (dimensions of force), u=Poisson’s ratio (dimensionless) and r=radius of the ring contact (dimensions of length).

Well, Summer was very mild in Southern California until the fire season broke out, in spades.  It looks like we’ll make it through this spate OK but that season is just beginning for us. 

Here’s wishing us all a terrific Autumn and getting the little ones back to school.  And here’s to all that broken glass that didn’t happen, this time.

Al H.
8-31-09